問題9（空間図形）※都立進学指導重点校入試プレ（中2）より

2023.05.25

オリジナル問題

下の図1に示した立体ABCD－EFGHは，AB＝8cm，BC＝BF＝6cm，DG＝10cmである直方体を表している。

点Pは，頂点Gを出発し，毎秒3cmの速さで辺GC，辺CB，辺BA 上を，G→C→B→Aの順に移動し，頂点Aに到着して止まる。点Pと頂点D，点Pと頂点F，点Pと頂点G，頂点Dと頂点F，頂点Dと頂点Gをそれぞれ結び，立体P－DFGをつくる。
次の各問に答えよ。

（問1）下の図2は，点Pが頂点Gを出発してから1秒後の状態を表している。このとき，立体P－DFGの体積は何cm³か。

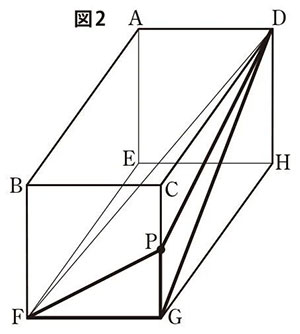
（問2）点Pが頂点Cと一致したとき，点Pから△DFGに下ろした垂線の長さは何cmか。

（問3）下の図3は，図1において辺DH上にある点をQとし，点Qと頂点D，点Qと頂点F，点Qと頂点Gをそれぞれ結び，立体Q－DFGをつくった場合を表している。

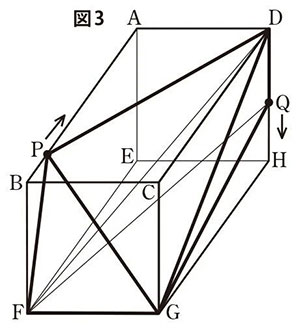
点Qは，点P が頂点Gを出発するのと同時に頂点Dを出発し，毎秒1cmの速さで辺DH上をD→Hの順に移動し，頂点Hに到着して止まる。
立体P－DFGと立体Q－DFGの体積が等しくなるのは，2点P，Qがそれぞれ頂点G，頂点Dを出発してから何秒後か。
ただし，2点P，Qがそれぞれ頂点G，頂点Dにあるときは考えないものとし，答えだけでなく，答えを求める過程が分かるように，途中の式や計算なども書け。

解答・解説はこちら

作問者からのメッセージ

中2対象の公開模試で出題した，直方体の辺上を動く点とそれによってできる三角錐に関する問題です。「線分と平面の位置関係を正確に捉える」ことがポイントです。また，「適切な平面を取り出して考える」「等しい角度に印を付ける」「状況に応じて図を描き直す」といった図形問題を解く上での基本が盛りだくさんに含まれていますので，解くだけでも勉強になる一問ではないかと思います。実際の模試では「高さ」となる線分を正確に捉えられていない答案が多く見られましたが，読者の皆さんは難なくクリアできるでしょうか。ぜひ，挑戦してみてください。