問題8（一次関数）※サピックスオープン（中3）より

2023.05.25

オリジナル問題

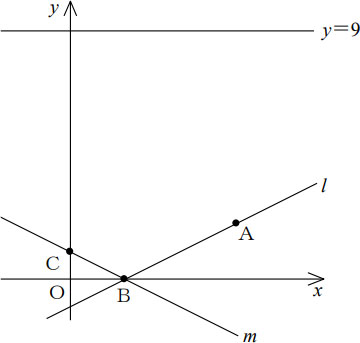
上の座標平面において，Ａ(6，2) を通り，傾きが 1 2 の直線lとx軸との交点をＢとする。
さらに，点Ｂを通り，傾きが－ 1 2 の直線mとy軸との交点をCとするとき，次の各問いに答えよ。

ACの中点の座標を求めよ。
△ABCの面積を求めよ。
次に，直線l，m，y＝9上にそれぞれ点P，Q，Rを，四角形BPRQがBP：BQ＝2：1の平行四辺形となるようにとるとき，その面積を求めよ。
ただし，点P，Qのいずれのy座標も正の数になるものとする。
【この問題は，答えに至るまでの途中過程や図を解法欄に記入すること】

作問者からのメッセージ

この問題は一次関数として出題しましたが，座標平面における平面図形（平行四辺形）の問題なので，平面図形の特徴を意識して解き進めることが必要です。実際の入試問題でも関数＋図形の出題は多く見られます。（3）では，答えまで辿りつく過程でほぼ相似しか使いません。平面図形の重要事項とともに，座標平面における基本知識も確認できる問題です。受験生の皆さんには，小問ごとのつながりと与えられた数値の意味を考えながら，そして出題者の意図を意識しながら解き進めてほしいと思っています。