問題2(平面図形)※サピックスオープン(中3)より
オリジナル問題
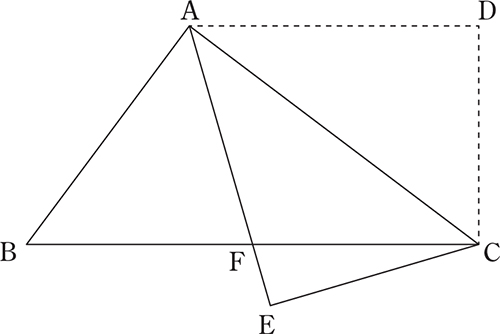
上の図は,AB=15,BC=25,AD=16,∠ADC=∠BCD=90°である台形ABCDにおいて,線分ACを折り目として△ADCを折り返した図形である。点Dの移った点をEとし,AEとBCとの交点をFとする。次の各問いに答えよ。
(1) 線分ACの長さを求めよ。
(2) △ACFの面積を求めよ。
(3) 線分BEの長さを求めよ。
作問者からのメッセージ
「折り返し図形」は図形の総合力を試すのに最適なテーマです。(1)(2)は基本問題ですが, (3)をどう解くか,これがこの問題のポイントです。力業で解くこともできますが,隠された図形的性質に気付けば一瞬で解けます。「解法にこだわりを持ってほしい」という思いを込めて作った1問です。皆さんも,ぜひ,悩み抜いてベストな解法を考えてみてください。
他の問題にチャレンジしたい方へ
【志望校合格力判定付】公開模試にチャレンジしたい方へ
SAPIXの公開模試は、最新の入試動向を反映し、徹底した問題分析のもとに作られたオリジナル模試です。難関校に合格した数多くの卒業生のデータに基づき、母集団の変動に左右されない精度の高い志望校合格力判定と、合格に向けた学習指針を示します。
