高校受験 数学解法研究（解き応えのあるオリジナル問題を公開中）

問題

一の位が0でない2けたの自然数nについて，「2乗して，求めた数の下2けたの値を答える」という操作を行います。
この操作を複数回行うときは，前の操作で求めた値に対して同じ操作を繰り返します。また，04のように操作後の十の位が0のときは，次の操作では一の位を2乗して値を求めるものとします。（この場合は4²=16）

例えば，n=54のとき，

1回操作を行うと，54²=2916 よって，16
2回操作を行うと，16²=256 よって，56
3回操作を行うと，56²=3136 よって，36

このとき，次の問いに答えなさい。

1. n=96のとき，4回操作を行ってつくられる値を求めなさい。
2. 1回操作を行って，つくられる値の一の位が6になるnは何個あるか求めなさい。
3. 1回操作を行って，96になるnの値をすべて求めなさい。
4. 2018回操作を行って，96になるnの値をすべて求めなさい。ただし，何回か操作を行って96になるnで，初めて96になるまで6回以上操作を行うものは存在しないことがわかっている。

• 2017年度実施「筑駒高入試プレ（中3）」より

1. ACの中点の座標を求めよ。
2. △ABCの面積を求めよ。
3. 次に，直線l，m，y＝9上にそれぞれ点P，Q，Rを，四角形BPRQがBP：BQ＝2：1の平行四辺形となるようにとるとき，その面積を求めよ。
   ただし，点P，Qのいずれのy座標も正の数になるものとする。
   【この問題は，答えに至るまでの途中過程や図を解法欄に記入すること】

• 2017年度実施「第1回 サピックスオープン（中3）」より

問題

下の図1に示した立体ABCD－EFGHは，AB＝8cm，BC＝BF＝6cm，DG＝10cmである直方体を表している。

点Pは，頂点Gを出発し，毎秒3cmの速さで辺GC，辺CB，辺BA 上を，G→C→B→Aの順に移動し，頂点Aに到着して止まる。点Pと頂点D，点Pと頂点F，点Pと頂点G，頂点Dと頂点F，頂点Dと頂点Gをそれぞれ結び，立体P－DFGをつくる。
次の各問に答えよ。

（問1）下の図2は，点Pが頂点Gを出発してから1秒後の状態を表している。このとき，立体P－DFGの体積は何cm³か。

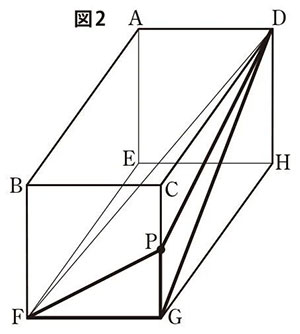
（問2）点Pが頂点Cと一致したとき，点Pから△DFGに下ろした垂線の長さは何cmか。

（問3）下の図3は，図1において辺DH上にある点をQとし，点Qと頂点D，点Qと頂点F，点Qと頂点Gをそれぞれ結び，立体Q－DFGをつくった場合を表している。

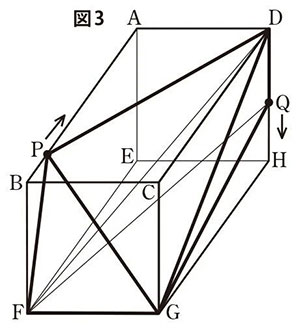
点Qは，点P が頂点Gを出発するのと同時に頂点Dを出発し，毎秒1cmの速さで辺DH上をD→Hの順に移動し，頂点Hに到着して止まる。
立体P－DFGと立体Q－DFGの体積が等しくなるのは，2点P，Qがそれぞれ頂点G，頂点Dを出発してから何秒後か。
ただし，2点P，Qがそれぞれ頂点G，頂点Dにあるときは考えないものとし，答えだけでなく，答えを求める過程が分かるように，途中の式や計算なども書け。

• 2017年度実施「都立進学指導重点校入試プレ（中2）」より

問題

ある自然数nについて，次のような作業を行います。

① nを12で割り，その商をさらに12で割る。商が0になるまでこれを繰り返す。
② ①の割り算を行った際に生じた余りを，右づめで続けて記録していく。割り切れたときは，余りが0であったものと考え，0を記録する。
③ 最終的に記録された数を【n】とする。

例えば，n＝564のとき，

564÷12＝47 余り0
47÷12＝3 余り11
3÷12＝0 余り3

となり，右から順に0，11，3が記録されるので，【n】＝3110 です。
このとき，次の問いに答えなさい。

1. 【n】＝345 であるとき，nの値を求めなさい。
2. 【n】＝1111 を満たす自然数nのうち，最小のものと最大のものをそれぞれ求めなさい。
3. 【n】が2017桁であるとき，n≦12^xを満たす自然数xのうち，最小のものを求めなさい。

• 2016年度実施「筑駒高入試プレ（中3）」より

問題は下記からご覧ください（PDF形式）。

• 2017年度実施「第3回 サピックスオープン（中2）」より

問題

下の図は，AB>AC の△ABCと，3点A，B，Cを通る円である。BCの延長とAを通る円の接線との交点をDとし，DA=DE となる点Eを辺BD上にとる。また，直線AEと円との交点のうち，Aとは異なる方をFとする。AE=4√5，BE=10，FE=3√5であるとき，次の問いに答えなさい。

1. ECの長さを求めなさい。
2. CDの長さを求めなさい。
3. AB:AC を求めなさい。
4. FCの長さを求めなさい。

• 2019年度実施「慶應女子高入試プレ（中3）」より

問題

上の図はある立体の展開図である。
BC=CD=DE=FG=GH=HJ=6，BF=CF=CG=DG=DH=EH=EJ=9 であるとき，この展開図を組み立ててできる立体について，以下の問いに答えよ。

1. この立体において，四角形CDHFの面積を求めよ。
2. この立体の各頂点を通る球Pの半径を求めよ。
3. この立体において，面ABCと面HIJの2 面間の距離を求めよ。
4. この立体の中に含まれる球Qの半径の値として考えられるもののうち，最も大きいものを求めよ。

• 2017年度実施「開成高入試プレ（中3）」より

問題

下の図のように，原点をOとする座標平面上の放物線 y=x²上にx座標が負である点Pをとり，Pを中心としてx軸と点Tで接する円Pをかく。円Pとy 軸との交点のうち，y 座標が大きいものから順にQ，Rとおき，直線PQと円Pとの交点のうち，x座標が小さい方をSとおく。また，直線PQとx軸との交点をA，放物線との交点のうちPでない方をBとおくと，AP:PB=4:5となった。
このとき，次の問いに答えよ。

1. 点Bからx軸に垂線BB’を下ろす。PT:BB’，TO:OB’をそれぞれ求めよ。
2. AP:PT，直線PQの傾きをそれぞれ求めよ。
3. 点P，点Bの座標をそれぞれ求めよ。
4. 点Rの座標を求めよ。
5. △STQ:△PRB を求めよ。

• 2016年度実施「開成高入試プレ（中3）」より

問題

上の図のように，BC=10 で，面積が50である△ABCの辺BC上に，BD=2，CE=4 となる2点D，Eをとる。また，辺AC上に AF:FC=3:5 となるような点Fをとる。さらに，線分EGで△ABCの面積を二等分するように，辺AB上に点Gをとる。
DFとEGとの交点をPとするとき，次の各問いに答えよ。

1. △ABC:△FDC を求めよ。
2. AG:GB を求めよ。
3. 四角形AGPFの面積を求めよ。

• 2016年度実施「サピックスオープン（中3）」より

問題

半径が6cmの球が2つあり，中心をO1，O2 とする。球O1 は正八面体ABCDEFに△ABE，△ABC，△ACD，△ADEで接し，球O2 は△FBE，△FBC，△FCD，△FDEで接しており，球O1 と△ABEの接点をPとおく。
2つの球O1，O2 が交わってできる円の直径の長さが4√6cmのとき，次の問いに答えなさい。

1. O1から面BCDEまでの距離を求めなさい。
2. 正八面体ABCDEFの1辺の長さを求めなさい。
3. 点Pを通り，△ACDに平行な平面でこの立体を切断するとき，球O1，球O2の切断面の面積を求めなさい。

• 2019年度実施「筑駒高入試プレ（中3）」より