【都立日比谷高攻略】数学の模試作問者が「視点・考え方」を語ります（問題付き）

作問者の視点と考え方を知ることは、入試で狙われるポイントや解法の理解に役立ちます。

そこで、今回はSAPIX公開模試の過去問題（数学）から、都立日比谷高の入試本番を想定したとっておきの一題を厳選。

作問者自らが、「なぜこの問題を出したのか」「難度をどう調整したのか」「受験生がどのように解くことを想定したのか」といった視点・考え方を紹介します。

難関高校を目指す受験生や、数学の実力を高めたい中学生はぜひ、今後の学習のヒントにしてください。

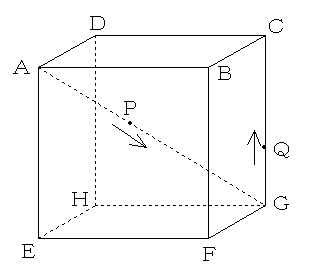
AB＝AE＝6，AD＝2√7の直方体ABCD－EFGH がある。

点Pは対角線AG上を毎秒5の速さでAからGまで動く。点Qは辺GC上を毎秒3の速さでGからCまで動く。点P，QはそれぞれA，Gを同時に出発し，点PがGに達したときに止まるものとする。

このとき，次の問いに答えよ。

1. ∠APQ＝90°になるのは出発してから何秒後か。
2. 点Pが△QHF上にくるのは出発してから何秒後か。
3. 2.のとき，立体ABPQの体積を求めよ。

• 早大学院入試プレ〈現 学校別サピックスオープン（早大学院）〉より

【作問者】木谷（SAPIX中学部 数学科）

青木　ここに載せたのは早大学院入試プレ〈現 学校別サピックスオープン（早大学院）〉の問題ですが、都立日比谷高を目指す受験生にも参考になるので紹介します。まずは本問を作った経緯からお願いします。

木谷　数学のテキストで、ある立体図形の切断の問題を見た時に、その問題で取り出していた対称面の形からインスピレーションを受けて作り始めました。また、動点の問題を苦手に感じる受験生が多いので、それも組み込みました。

青木　対称面を取り出せない受験生も意外と多いので、（1）に対称面を取るという、極めて基本的な作業を入れたのは良いアイデアですね。

作問する際、ご自分なりのルールは設けていますか。例えば、授業で生徒が間違えた箇所もきっかけになるのでしょうか。

木谷　授業中に生徒が間違えた問題や、難しいと感じていた点はメモを取っていて、模試にそれらの内容を反映することはあります。ただし、私が思い付いた問題が、受験生にとっては難しすぎる場合もあるので、なるべくそこが乖離しないようにしています。

青木　本問はどの程度の難度なのでしょうか。

木谷　本問は標準的な難度で、都立日比谷高や早慶高を志望する受験生には対応してほしいです。都立日比谷高の立体図形の問題はシンプルな設定が多く、ここ数年は錐体の問題がよく出ています。近年では柱体についても出題されたので、今回ご紹介した問題は入試対策になると思います。問題そのもののシンプルさ、相似を使うところも都立日比谷高の入試問題に似ています。

青木　解答時間の目安はどれくらいでしょうか。

木谷　10分くらいです。

【聞き手】青木（SAPIX中学部 数学科教科長）

青木　立体図形を難しく感じる生徒は多いと思います。注意点はありますか。

木谷　立体図形は「適切な平面を取り出して、平面図形の問題として捉える」と対応しやすくなると伝えています。

その平面をどのように取り出すかというのが、立体図形のテーマでもあります。本問は対称面を取り出すことができれば、解きやすくなります。空間内の体積を求める問題もありますが、平面図形の要素を使うことは多いでしょう。

青木　難関校では立体図形の問題が満遍なく出されていますね。

木谷　はい。しかも、得点源になることが多いですね。都立進学指導重点校でも、学校ごとに傾向が違うとはいえ、立体図形の問題を解くことは入試対策として欠かせないでしょう。

青木　この問題では、（1）の解答の流れから（2）を解くのではなく、（1）と（2）が別物のように存在していますが、あえて小問ごとに設定を変えようと意識したのですか。

木谷　はい。都立進学指導重点校の自校作成問題に多いパターンですね。ただし、実はこの問題は（1）と（2）で設定こそ違いますが、「適切な平面を取り出してみよう」というメッセージは同じです。（1）では「△ACG」、（2）では「平面AEGC」を取り出すのがポイントです。（1）に取り組みやすい問題を出して、平面を取り出しやすくすることで、（2）も「平面を取り出す問題なのでは」と気付きやすくしています。

青木　苦手意識が強い受験者も、練習次第で対処できますね。

木谷　図形問題に限らず、問題への考え方やアプローチの仕方をしっかり身に付けておくことが大切なポイントだと思います。

青木　ところで、（3）は複数の解き方がありますね。私は模範解答と違う解き方をしていました。

木谷　実は、私も最初は別のアプローチを想定していました。しかし、模試討議（※）の場で、「この解法の方が良いのでは」と提案され、採用することにしたのです。

青木　模試討議では相当議論し、意見交換しますよね。この模範解答が選ばれたポイントはどのようなところだったのですか。

木谷　「受験生が思いつきやすいもの」がベストのときもありますが、本問は「受験生のその後の学習において特に有益だと考えた解法」を模範解答として採用しています。

青木　受験生もさらに高いレベルを目指すなら、ある程度、一定の解法を押さえた上で、自分で多様な発想をしてみるのも大事ですよね。

木谷　諦めずに、自分なりの発想で問題に取り組む姿勢も大切です。

青木　本日はありがとうございました。

• 模試討議：教科ごとに複数の講師が集まり、模試の内容について検討・議論すること。