【開成高攻略】数学の模試作問者が「視点・考え方」を語ります(問題付き)
インタビューオリジナル問題
作問者の視点と考え方を知ることは、入試で狙われるポイントや解法の理解に役立ちます。
そこで、今回はSAPIX公開模試の過去問題(数学)から、開成高の入試本番を想定したとっておきの一題を厳選。
作問者自らが、「なぜこの問題を出したのか」「難度をどう調整したのか」「受験生がどのように解くことを想定したのか」といった視点・考え方を紹介します。
難関高校を目指す受験生や、数学の実力を高めたい中学生はぜひ、今後の学習のヒントにしてください。
①まずは問題にチャレンジしてみよう(目標解答時間:15分)
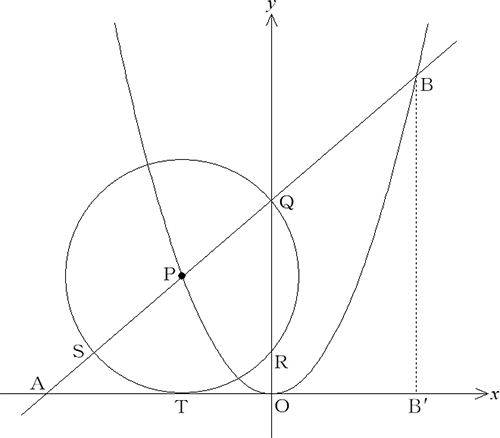
問題〈テーマ:関数と円〉
図のように,原点をOとする座標平面上の放物線y=X2上にx座標が負である点Pをとり,Pを中心としてx軸と点Tで接する円Pをかく。
円Pとy軸との交点のうち,y座標が大きいものから順にQ,Rとおき,直線PQと円Pとの交点のうち,x座標が小さい方をSとおく。
また,直線PQとx軸との交点をA,放物線との交点のうちPでない方をBとおくと,AP:PB=4:5となった。このとき,次の問いに答えよ。
- 点Bからx軸に垂線BB’を下ろす。PT:BB’ ,TO:OB’をそれぞれ求めよ。
- AP:PT,直線PQの傾きをそれぞれ求めよ。
- 点P,点Bの座標をそれぞれ求めよ。
- 点Rの座標を求めよ。
- △STQ:△PRB を求めよ。
- 開成高入試プレ〈現 学校別サピックスオープン(開成高)〉より
②作問者の視点・考え方を知ろう

【作問者】藤原(SAPIX中学部 数学科)
青木 この問題を作った経緯を教えてください。
藤原 開成高に限らず、入試では時間をかけて難問で正答するより、基本的な問題でミスなく得点する方が合否に直結することが多いのです。そのため、標準的な内容を組み合わせて、本問を作りました。
しかし、正答率は(1)こそ90%を超えましたが、(2)は比の問題、傾きの問題ともに50%ずつぐらい、(3)(4)は共に30%強で、(5)が14%と、(2)以降は伸びませんでした。
青木 作問者として、この正答率をどう思われますか。
藤原 想定を下回りました。(1)~(3)は70%くらいの正答率を想定し、円の性質を使った(4)から正答率が下がると考えていました。特に、(2)は「2つの異なる比を1つの比に統一する(直す)だけ」という意識で作ったので、受験生の約半数が正答できなかったのは意外でした。
青木 (2)から(3)は決して難しくないですし、解き方も分かりやすく誘導されているので、そのとおりにアプローチしていけば解けるように見えます。
藤原 例えば、(2)は「AP:PQ」を求める問題にし、その後に「直線PQの傾き」を聞けば、正答率は上がったかもしれません。
青木 そこまで誘導するのも、親切すぎる気がします。(1)~(5)を通して別解はありますか。
藤原 (5)だけですね。そのまま計算するか、比を使って解くかというくらいです。
青木 (5)はPT=QRに気付かず、普通に計算したとしても、さほど時間はかからないはずですが、苦戦した受験生が多かったようですね。普段作問するとき、自分なりのルールはありますか。
藤原 「たまたま思い付きで解けてしまった」など、一発逆転系にならないよう注意しています。こつこつ勉強してきた受験生だからこそ得点できたという問題の方が良いと思うからです。

【聞き手】青木(SAPIX中学部 数学科教科長)
青木 本問はかっちりとした誘導形式の問題ですが、この形式にした理由はありますか。
藤原 普段扱っているSAPIXのテキストでも、例えば前半の設問の(1)(2)が、後半の設問の(3)につながるような誘導形式が多く掲載されています。しかし、その誘導に気付かず、各小問を別物として捉える生徒が少なくないのです。
そのため、「さすがに開成高の志望者なら、作問者が仕組んだ誘導を見落とさないでほしい」という想いを込めて本問を作りました。
青木 授業をしていると、むしろ誘導に気付く生徒の方が少ないときもありますね。(1)~(5)までの解答時間の目安はどのくらいでしょうか。
藤原 受験生によってはこの大問全てを10分かけずに解き終えます。開成高の入試では大問4問を60分で解かなければならないので、1問にかけられる時間は最大で15分程度。むしろ、10分で解き終えて、余った時間を他の問題に充ててほしいですね。
青木 ところで、受験生が(2)を解けなかった要因は何であったと考えていますか。
藤原 考えられるのは、「PTとPQの長さ」が同じである点に気付いていないことです。「X軸上のTO:OB’」という地面の比と、斜めの比があって、(1)でそれをそろえるという作業があります。その作業を思い付けなかったものと考えています。
ただし、本問だけを取り上げ、15分の時間制限を設けたら、全て解き終える受験生はより増えるはずです。模試では他の問題との兼ね合いで、本問に十分なリソースを割けなかった受験生も多かったでしょう。
青木 厳しい選択が求められますね。
藤原 こうした制限下でも解答できるよう、普段の授業では「(1)を使って(2)をどう解くか」「(3)を解くに当たり、(1)(2)の結果は使えないだろうか」など、小問の流れを意識するのが大事だと伝えています。
青木 問題で何を聞かれているのかをきちんと理解してから、解答の流れを見いだしていくことが大切ですね。
藤原 本問で言えば、いきなり(4)に挑んでも、解答に至るまでのステップが多く、より難しく感じるでしょう。順々に誘導して、最後に最も重要な結論が出るような問題が作られるケースは多く、意味のない小問は基本的にないと考えた方が安全でしょう。
青木 開成高を志望せずとも、早慶高レベルを目指すのなら、本問のような問題を最後まで解けるようにしてほしいですね。
藤原 はい。ただし、大問によっては(1)と(2)で設定が変わり、全く別物になるケースも大いにあります。それだけに、問題文を読む段階で、「どんな聞かれ方をしているのか」「使っていない条件はないか」「図に書き込みが漏れていないか」などを確認することが重要です。
青木 本日はありがとうございました。
