問題5（場合の数）※サピックスチャレンジテスト（新中3）より

花子：「数えるのは大変そうね。ひとまず4人のときや5人のときから考えて，その中で計算方法を見つけていきましょうか。」
太郎：「うん。まずは4人の場合から。これは樹形図でも数えやすいね。とりあえず答えは【ア】通りになるかな。」
花子：「そうだね。じゃあ，それを計算で求める方法を考えてみましょう。実際にプレゼント交換をする場合，どう交換すればよさそう？」
太郎：「例えば4人をＡ～Ｄとすると，このように輪になってＡのプレゼントをＢに，ＢのプレゼントをＣに，ＣのプレゼントをＤに，ＤのプレゼントをＡに，って感じに，『輪になって各々が右隣の人に渡す』のはどうかな？」

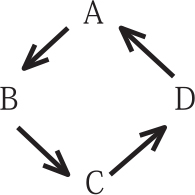
花子：「うん，いいね。この場合，4人が輪になるような並べ方が何通りになるか考えればよさそうね。」
太郎：「この並べ方って，誰か1人から見える他3人の位置が変われば別の並べ方とみなせるから，Ａの右隣，正面，左隣に来る人が何通りかをそれぞれ考えればいいよね。Ａの右隣に来る人は【イ】通り，正面は【ウ】通り，左隣は【エ】通りだから，この交換の仕方は【オ】通り。あれ？【ア】通りにならないよ。」
花子：「待って。別に輪にならなくても，4人をいくつかのグループに分けて，その中で交換してもいいよね。例えばこんな感じに　(Ａ，Ｂ) と (Ｃ，Ｄ) に『組分け』して，ＡとＢのプレゼントを交換して，ＣとＤのプレゼントを交換するって形ね。」

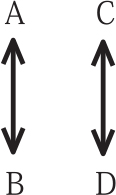
太郎：「あ，確かに。今回の場合は2人，2人の組分けだけ考えればいいかな。4人を2人，2人に分ける場合の数は，4人から1つ目の組にする2人を選べば，残りの2人がそのまま2組目になれるわけだから，6通りでいいのかな。」
花子：「いえ，それだと例えば，『①最初にＡ，Ｂを選んだ場合』と『②最初にＣ，Ｄを選んだ場合』が結局同じ分け方になって重複しちゃうよね。①と②は組のできる順番を並び替えただけでしょ。他の選び方についても同様のことが言えるから，要するに各組の人数が同じ場合には，『組の並び替え方の分だけ重複が発生する』んじゃないかしら。」
太郎：「そうか。組の並び替え方は2通りだから，組分けの場合の数は6÷2＝3通りになって，それぞれの交換の仕方が1通りずつだから，この方法での交換は3×1×1＝3通り。だから，合計で【ア】通りになるんだ！」
花子：「うん，答えと一致したね。この考え方を使えば，他の人数でも計算で求められそうね。試しに5人の場合でもやってみましょう。」

花子：「まず，『輪になって各々が右隣の人に渡す』やり方を方法Ⅰとすると，この場合は【カ】通りね。」
太郎：「うん，じゃあ次は『組分けする』やり方だね。これを方法Ⅱとすると，今回は2人組と3人組に分けることになるから，その分け方は【キ】通り。それぞれの組での交換の仕方は，2人組の方は互いに渡し合うだけだから1通りだけど，3人組の方はどうなるんだろう？」
花子：「その3人で方法Ⅰを使えばいいのよ。だから3人組の交換の仕方は【ク】通りね。」
太郎：「なるほど！ということは方法Ⅱでの交換は【ケ】通り。だから，合計して【コ】通りかな。」
花子：「うん，あってる！じゃあ，6人の場合も計算してみましょう！」

作問者からのメッセージ

プレゼント交換の場合の数に代表される「完全順列（攪乱順列）」について，樹形図で書きだす以外のアプローチの一つを示した問題になります。場合の数は，問題の捉え方次第でさまざまなアプローチが考えられます。プレゼント交換を「床に置いたものの中から1人ずつ取っていく」と捉えるか，「手渡しで誰かと交換していく」と捉えるかで発想が変わります。この問題では「樹形図以外のアプローチを学ぶ」ことに加え，場合の数の基本である「積の法則・和の法則の使い分け」，「重複の可否の判断」などといった事項の確認もできますので，ぜひ，チャレンジしてください。